Matrix multiplication is a fundamental operation in various computational fields, including computer graphics, machine learning, and scientific computing. Given matrices A (of size m × n) and B (of size n × p), the resulting matrix C = A × B has a size of m × p. The naive algorithm has a time complexity of O(n3), which can be slow for large matrices. This document explores various techniques to optimize matrix multiplication.
The naive approach involves three nested loops, iterating over rows of A and columns of B, and computing the sum of products for each element in C. This approach, though straightforward, has poor cache locality and lacks optimization.
void naive_multiplication(const std::vector<int32_t>& A, const std::vector<int32_t>& B, std::vector<int32_t>& C, int32_t m, int32_t n) {
for (int32_t i = 0; i < m; i++) {
for (int32_t j = 0; j < n; j++) {
C[i * n + j] = 0;
for (int32_t k = 0; k < n; k++) {
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
Tiling (also called blocking) improves cache locality by dividing the matrices into smaller blocks (or tiles) that fit into the cache. Processing tiles instead of the entire matrix reduces cache misses and improves memory access patterns.
void tiled_multiplication(const std::vector<int32_t>& A, const std::vector<int32_t>& B, std::vector<int32_t>& C, int32_t m, int32_t n, int32_t tile_size) {
for (int32_t i = 0; i < m; i += tile_size) {
for (int32_t j = 0; j < n; j += tile_size) {
for (int32_t k = 0; k < n; k += tile_size) {
for (int32_t ii = i; ii < std::min(i + tile_size, m); ii++) {
for (int32_t jj = j; jj < std::min(j + tile_size, n); jj++) {
int32_t sum = 0;
for (int32_t kk = k; kk < std::min(k + tile_size, n); kk++) {
sum += A[ii * n + kk] * B[kk * n + jj];
}
C[ii * n + jj] += sum;
}
}
}
}
}
}
Loop unrolling reduces loop overhead by manually unrolling the innermost loop, enabling the processor to execute instructions in parallel. This technique is effective for increasing instruction-level parallelism, but it doesn't improve cache locality.
void loop_unrolled_multiplication(const std::vector<int32_t>& A, const std::vector<int32_t>& B, std::vector<int32_t>& C, int32_t m, int32_t n) {
for (int32_t i = 0; i < m; i++) {
for (int32_t j = 0; j < n; j++) {
C[i * n + j] = 0;
int32_t k = 0;
for (; k <= n - 8; k += 8) { // Unrolled by factor of 8
C[i * n + j] += A[i * n + k] * B[k * n + j];
C[i * n + j] += A[i * n + k + 1] * B[(k + 1) * n + j];
C[i * n + j] += A[i * n + k + 2] * B[(k + 2) * n + j];
C[i * n + j] += A[i * n + k + 3] * B[(k + 3) * n + j];
C[i * n + j] += A[i * n + k + 4] * B[(k + 4) * n + j];
C[i * n + j] += A[i * n + k + 5] * B[(k + 5) * n + j];
C[i * n + j] += A[i * n + k + 6] * B[(k + 6) * n + j];
C[i * n + j] += A[i * n + k + 7] * B[(k + 7) * n + j];
}
// Handle any remaining elements
for (; k < n; k++) {
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
OpenMP can be combined with tiling to leverage multi-core processors. This approach assigns tiles to different threads, which can operate independently, thus improving performance on multi-threaded systems.
#include <omp.h> // Include for OpenMP
void parallel_tiled_multiplication(const std::vector<int32_t>& A, const std::vector<int32_t>& B, std::vector<int32_t>& C, int32_t m, int32_t n, int32_t tile_size) {
#pragma omp parallel for collapse(2) num_threads(NUM_THREADS)
for (int32_t i = 0; i < m; i += tile_size) {
for (int32_t j = 0; j < n; j += tile_size) {
for (int32_t k = 0; k < n; k += tile_size) {
for (int32_t ii = i; ii < std::min(i + tile_size, m); ii++) {
for (int32_t jj = j; jj < std::min(j + tile_size, n); jj++) {
int32_t sum = 0;
for (int32_t kk = k; kk < std::min(k + tile_size, n); kk++) {
sum += A[ii * n + kk] * B[kk * n + jj];
}
#pragma omp atomic
C[ii * n + jj] += sum;
}
}
}
}
}
}
AVX-512 is an Intel SIMD (Single Instruction, Multiple Data) extension that allows processing multiple data elements simultaneously. By using AVX-512 intrinsics, we can vectorize matrix multiplication, significantly improving performance.
#include <immintrin.h> // Include for AVX512 intrinsics
void avx512_multiplication(const std::vector<int32_t>& A, const std::vector<int32_t>& B, std::vector<int32_t>& C, int32_t m, int32_t n) {
for (int32_t i = 0; i < m; i++) {
for (int32_t j = 0; j < n; j++) {
__m512i c = _mm512_setzero_si512(); // Accumulator for result
for (int32_t k = 0; k < n; k += 16) {
__m512i a = _mm512_loadu_si512(&A[i * n + k]);
__m512i b = _mm512_loadu_si512(&B[k * n + j]);
__m512i prod = _mm512_mullo_epi32(a, b);
c = _mm512_add_epi32(c, prod);
}
int32_t result[16];
_mm512_storeu_si512(result, c);
C[i * n + j] = 0;
for (int x = 0; x < 16; x++) {
C[i * n + j] += result[x];
}
}
}
}
AVX-512 is an Intel SIMD (Single Instruction, Multiple Data) extension that allows processing multiple data elements simultaneously. By using AVX-512 intrinsics, we can vectorize matrix multiplication, significantly improving performance.
#include <immintrin.h> // Include for AVX512 intrinsics
#include <omp.h> // Include for OpenMP
void avx512_par_multiplication(const std::vector& A, const std::vector& B, std::vector& C, int32_t m, int32_t n)
{
#pragma omp parallel for collapse(2) num_threads(NUM_THREADS)
for (int32_t i = 0; i < m; i++) {
for (int32_t j = 0; j < n; j++) {
__m512i c = _mm512_setzero_si512(); // Accumulator for result
for (int32_t k = 0; k < n; k += 16) {
// Load 16 elements from row of A and column of B
__m512i a = _mm512_loadu_si512(&A[i * n + k]);
__m512i b = _mm512_loadu_si512(&B[k * n + j]);
// Multiply and accumulate into c
__m512i prod = _mm512_mullo_epi32(a, b);
c = _mm512_add_epi32(c, prod);
}
// Horizontal sum of the 16 integers in c
int32_t result[16];
_mm512_storeu_si512(result, c);
C[i * n + j] = 0;
for (int x = 0; x < 16; x++) {
C[i * n + j] += result[x];
}
}
}
}
This technique combines AVX-512, tiling, and OpenMP parallelization. By breaking down matrices into tiles and vectorizing operations within each tile, we maximize both data locality and parallelism.
#include <immintrin.h> // Include for AVX512 intrinsics
#include <omp.h> // Include for OpenMP
void avx512_tiled_multiplication(const std::vector<int32_t>& A, const std::vector<int32_t>& B, std::vector<int32_t>& C, int32_t m, int32_t n, int32_t tile_size) {
#pragma omp parallel for collapse(2) num_threads(NUM_THREADS)
for (int32_t i = 0; i < m; i += tile_size) {
for (int32_t j = 0; j < n; j += tile_size) {
for (int32_t k = 0; k < n; k += tile_size) { // Tile for the 'kk' dimension
for (int32_t ii = i; ii < std::min(i + tile_size, m); ii++) {
for (int32_t jj = j; jj < std::min(j + tile_size, n); jj++) {
__m512i c = _mm512_setzero_si512(); // Accumulate in 512-bit registers
for (int32_t kk = k; kk < std::min(k + tile_size, n); kk += 16) {
__m512i a = _mm512_loadu_si512(&A[ii * n + kk]);
__m512i b = _mm512_loadu_si512(&B[kk * n + jj]);
__m512i prod = _mm512_mullo_epi32(a, b);
c = _mm512_add_epi32(c, prod);
}
int32_t result[16];
_mm512_storeu_si512(result, c);
if (k == 0) C[ii * n + jj] = 0; // Initialize to zero only once
for (int x = 0; x < 16; x++) {
C[ii * n + jj] += result[x];
}
}
}
}
}
}
}
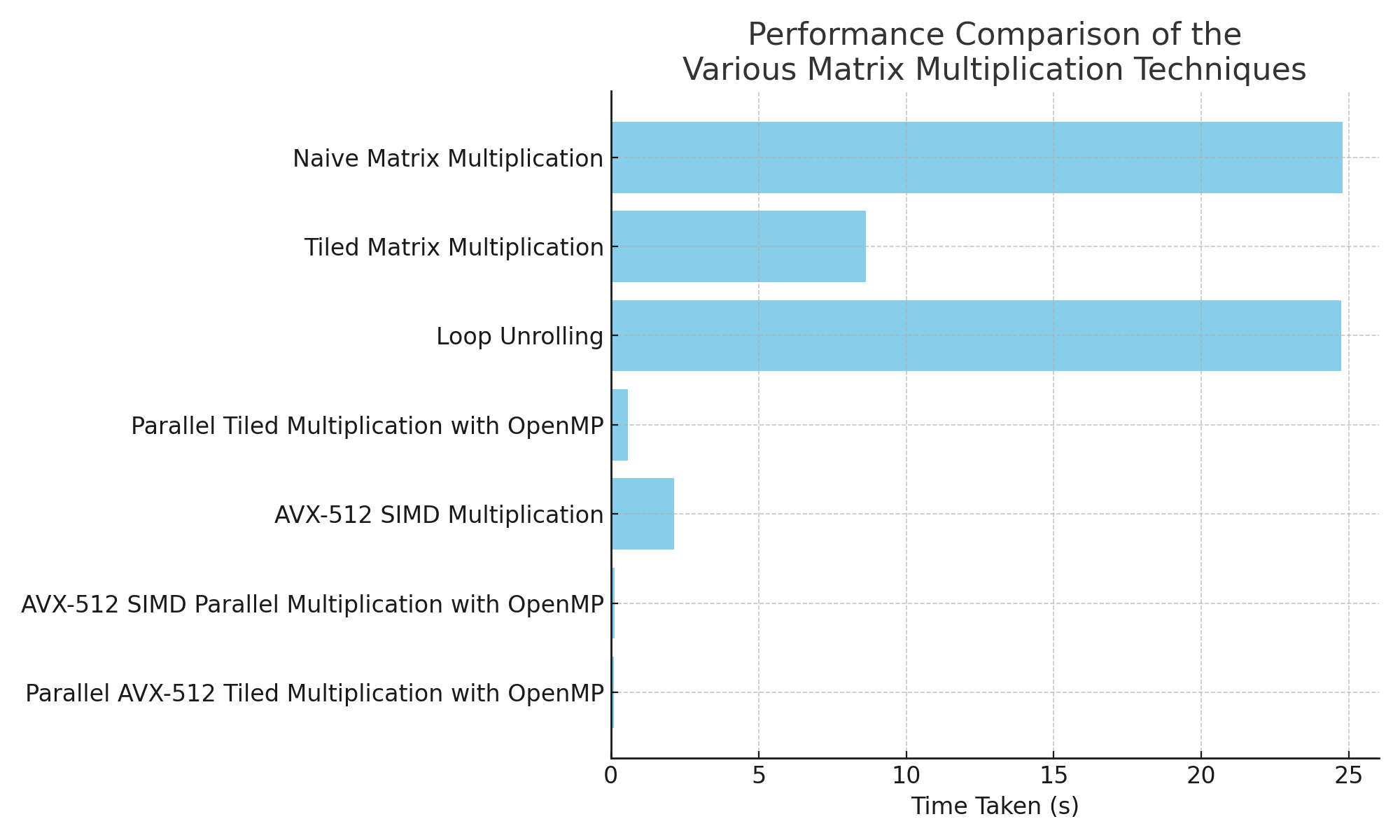
For the following experiments, we used the following hardware and software configuration:
-O3 compiler flag322048 x 2048Intel(R) Xeon(R) Gold 6242R CPU @ 3.10GHz with two sockets (20 cores per socket, totaling 40 cores)The chart below shows the time taken by each matrix multiplication method under these experimental conditions.