Prefix sum (or scan) is a foundational operation in parallel computing. It computes cumulative sums over an array, enabling efficient algorithms for sorting, searching, and many other applications. This blog demonstrates various CUDA implementations of prefix sum on an NVIDIA A100 GPU, showcasing the advantages of shared memory and dynamic parallelism.
The prefix sum of an array \( A \) produces an array \( S \), where:
\( S[i] = A[0] \oplus A[1] \oplus \dots \oplus A[i] \) for \( i \geq 0 \),
and \( \oplus \) is any associative operator (e.g., addition, multiplication, or bitwise AND).
The recursive definition of the prefix sum is:
\( S[i] = \begin{cases} A[0] & \text{if } i = 0, \\ S[i-1] \oplus A[i] & \text{if } i > 0. \end{cases} \)
While addition (\( + \)) is used in this implementation, the approach generalizes to any associative operation.
Understanding how GPUs work is crucial to optimizing parallel algorithms like prefix sum. Let’s break down the key architectural concepts using the NVIDIA A100 GPU as an example:
An NVIDIA A100 GPU contains 108 Streaming Multiprocessors (SMs). Each SM acts as a mini-processor, capable of executing multiple threads simultaneously. Within an SM:
Threads are the smallest unit of execution in a GPU. In CUDA:
For example, if a thread block contains 1024 threads, it will be divided into \( 1024 / 32 = 32 \) warps.
Threads are grouped into blocks, and blocks are organized into a grid. Each block executes independently, with shared memory facilitating communication among threads within a block.
For example, to process an array of 1 million elements with 1024 threads per block, we need \( \lceil 10^6 / 1024 \rceil = 976 \) blocks. These blocks are distributed across the 108 SMs of the A100.
Optimizing memory usage (e.g., minimizing global memory accesses) is critical for performance.
To efficiently compute prefix sums on a GPU, we leverage the parallel nature of CUDA. The key idea is to divide the computation into multiple steps, updating the array in-place with increasing strides. Here’s a step-by-step breakdown:
Each thread copies a portion of the array from global memory into shared memory, allowing fast access during computation.
Using a stride-based approach, each thread computes its local prefix sum by combining values within its segment of the array:
\( A[i] = A[i] \oplus A[i - \text{stride}] \)
This is repeated for increasing strides (\( \text{stride} = 1, 2, 4, \dots \)) until the entire block is processed.
Since blocks compute prefix sums independently, their results must be adjusted to reflect the cumulative sums of preceding blocks. This requires a second phase or dynamic parallelism.
These implementations are designed for intra-block prefix sums:
This implementation computes prefix sums sequentially within a parallel kernel, making it inefficient on GPUs:
__global__ void naive_prefix_sum(int *input, int n) {
int tid = threadIdx.x + blockIdx.x * blockDim.x;
if (tid == 0) return;
for (int i = 1; i < n; ++i) {
if (tid == i) {
input[tid] += input[tid - 1];
}
__syncthreads();
}
}
This kernel uses \( O(\log n) \) steps but relies on slow global memory access:
__global__ void global_prefix_sum(int *input, int n) {
int tid = threadIdx.x + blockIdx.x * blockDim.x;
for (int step = 1; step < n; step *= 2) {
int temp = (tid >= step) ? input[tid - step] : 0;
__syncthreads();
if (tid < n) {
input[tid] += temp;
}
__syncthreads();
}
}
This kernel leverages shared memory for faster intra-block communication:
__global__ void shared_prefix_sum(int *input, int n) {
__shared__ int shared_mem[1024]; // Shared memory array
int tid = threadIdx.x + blockIdx.x * blockDim.x;
// Load data into shared memory
if (tid < n) {
shared_mem[threadIdx.x] = input[tid];
} else {
shared_mem[threadIdx.x] = 0;
}
__syncthreads();
for (int step = 1; step < blockDim.x; step *= 2) {
int temp = (threadIdx.x >= step) ? shared_mem[threadIdx.x - step] : 0;
__syncthreads();
shared_mem[threadIdx.x] += temp;
__syncthreads();
}
// Write results back to global memory
if (tid < n) {
input[tid] = shared_mem[threadIdx.x];
}
}
The computation of prefix sums across multiple blocks requires handling inter-block dependencies. Two methods address this challenge:
The computation is divided into two kernels:
This method is efficient but involves overhead due to launching multiple kernels and synchronizing between them.
This approach uses dynamic parallelism to launch the adjustment kernel directly from the device:
This method is faster because it eliminates the need for the host to manage inter-block adjustments, making it ideal for workloads with significant inter-block dependencies.
This method splits the computation into two kernels: one for local prefix sums and another for adjustments across blocks.
__global__ void compute_local_prefix_sum(int *input, int *block_sums, int n) {
__shared__ int shared_mem[1024];
int tid = threadIdx.x + blockIdx.x * blockDim.x;
// Compute local prefix sum
if (tid < n) {
shared_mem[threadIdx.x] = input[tid];
} else {
shared_mem[threadIdx.x] = 0;
}
__syncthreads();
for (int step = 1; step < blockDim.x; step *= 2) {
int temp = (threadIdx.x >= step) ? shared_mem[threadIdx.x - step] : 0;
__syncthreads();
shared_mem[threadIdx.x] += temp;
__syncthreads();
}
if (tid < n) {
input[tid] = shared_mem[threadIdx.x];
}
// Store the block sum
if (threadIdx.x == blockDim.x - 1) {
block_sums[blockIdx.x] = shared_mem[threadIdx.x];
}
}
__global__ void adjust_block_sums(int *input, int *block_sums, int n) {
int tid = threadIdx.x + blockIdx.x * blockDim.x;
// Adjust with preceding block sums
if (blockIdx.x > 0 && tid < n) {
input[tid] += block_sums[blockIdx.x - 1];
}
}
Dynamic parallelism enables a kernel to launch another kernel for inter-block adjustments:
__global__ void dynamic_prefix_sum(int *input, int *block_sums, int n) {
int tid = threadIdx.x + blockIdx.x * blockDim.x;
__shared__ int shared_mem[1024];
if (tid < n) {
shared_mem[threadIdx.x] = input[tid];
} else {
shared_mem[threadIdx.x] = 0;
}
__syncthreads();
for (int step = 1; step < blockDim.x; step *= 2) {
int temp = (threadIdx.x >= step) ? shared_mem[threadIdx.x - step] : 0;
__syncthreads();
shared_mem[threadIdx.x] += temp;
__syncthreads();
}
if (tid < n) {
input[tid] = shared_mem[threadIdx.x];
}
if (threadIdx.x == blockDim.x - 1) {
block_sums[blockIdx.x] = shared_mem[threadIdx.x];
}
// Launch adjustment kernel dynamically
if (blockIdx.x == gridDim.x - 1 && threadIdx.x == 0) {
adjust_block_sums<<>>(input, block_sums, n);
}
}
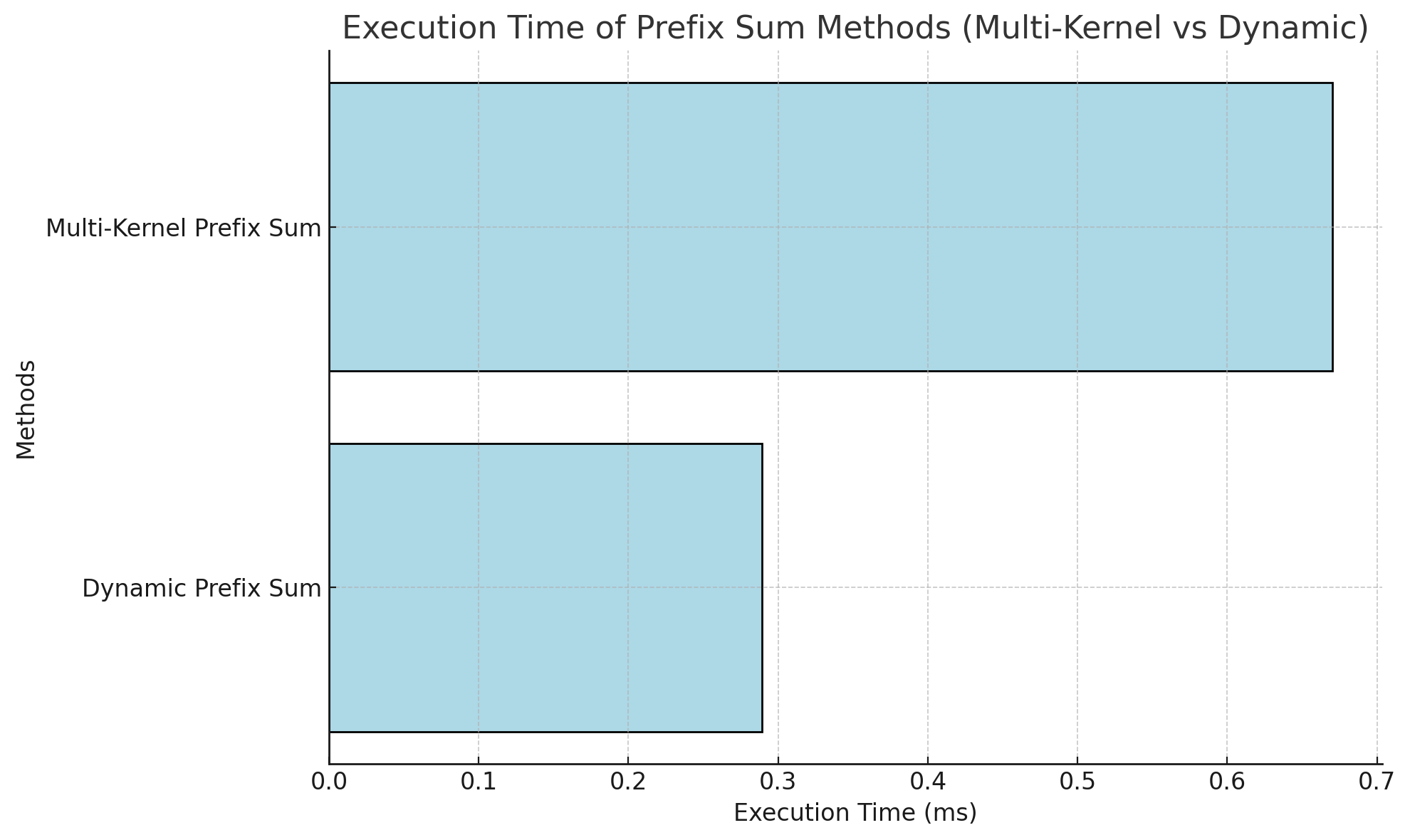
In summary, Dynamic Parallelism outperforms Multi-Kernel Prefix Sum by reducing the dependency on the host for managing inter-block adjustments. This results in lower latency and better scalability for large-scale parallel workloads.

The chart above compares the performance of different prefix sum methods, demonstrating the efficiency of shared memory and dynamic parallelism for managing inter-block dependencies.
Optimizing prefix sum computation on GPUs requires careful consideration of memory access patterns, inter-block communication, and parallel execution. Dynamic parallelism and shared memory optimizations showcase the power of modern GPUs like the NVIDIA A100 in efficiently solving parallel problems.
Harris, Mark, Sengupta, Shubhabrata, & Owens, John D. Chapter 39. Parallel Prefix Sum (Scan) with CUDA. In GPU Gems 3, Part VI: GPU Computing. NVIDIA Corporation. https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-39-parallel-prefix-sum-scan-cuda.