Roofline Analysis of Matrix Multiplication (INT32)

Introduction

Roofline analysis is a visual model for evaluating the performance of computational workloads, particularly matrix multiplication. In this blog, we analyze the performance of naive and SIMD (Single Instruction Multiple Data) implementations of matrix multiplication for 32-bit integers (INT32) on a dual-socket Intel Xeon Gold 6248R processor.

Hardware Specifications and Compute Hardware AI

The experiments were conducted on a dual-socket Intel Xeon Gold 6248R processor with the following specifications:

• Cores: 24 cores per socket, 48 cores in total.
• Base Frequency: 3.0 GHz.
• Peak Performance: 288 GFLOPS (32-bit integer operations).
• Memory Bandwidth: 281.4 GB/s (dual-socket).

The hardware Arithmetic Intensity (AI) is given by:
Hardware AI = Compute Roof / Memory Bandwidth

Substituting the values:
Hardware AI = 288 GFLOPS / 281.4 GB/s ≈ 1.02 FLOPs/byte

Problem Setup and Theoretical AI

The problem involves multiplying two square matrices of size N = 8192. Each element in the resulting matrix involves:

• 8192 multiplications
• 8191 additions

Total FLOPs for the operation:

FLOPs = 2 × N³ = 2 × 8192³ = 1.099 trillion FLOPs
        

Bytes Transferred:

Matrix A: 8192 × 8192 × 4 bytes = 256 MB
Matrix B: 8192 × 8192 × 4 bytes = 256 MB
Matrix C: 8192 × 8192 × 4 bytes = 256 MB
Total Bytes = 768 MB
        

Theoretical AI based on the problem:
Theoretical AI = FLOPs / Bytes Transferred = 1099511627776 / (768 × 1024 × 1024) ≈ 1365.33 FLOPs/byte

Naive Matrix Multiplication

The naive implementation uses three nested loops:

for (int i = 0; i < N; i++) {
    for (int j = 0; j < N; j++) {
        int32_t sum = 0;
        for (int k = 0; k < N; k++) {
            sum += A[i * N + k] * B[k * N + j];
        }
        C[i * N + j] = sum;
    }
}
        

Performance metrics for the naive implementation:
Naive GFLOPS/sec = 5.7 GFLOPS
Naive AI = 0.249985 FLOPs/byte

SIMD Matrix Multiplication

The SIMD implementation leverages AVX-512 to process 16 elements simultaneously:

for (int k = 0; k < N; k += 16) {
    __m512i a = _mm512_loadu_si512(&A[i * N + k]);
    __m512i b = _mm512_loadu_si512(&B[k * N + j]);
    __m512i prod = _mm512_mullo_epi32(a, b);
    c = _mm512_add_epi32(c, prod);
}
        

Performance metrics for the SIMD implementation:
SIMD GFLOPS/sec = 45.6 GFLOPS
SIMD AI = 0.249985 FLOPs/byte

Why SIMD is Faster Despite Same AI

Both naive and SIMD implementations have the same Arithmetic Intensity (AI) of 0.249985 FLOPs/byte. This is because the amount of computation (FLOPs) and memory transfers (bytes) are identical in both cases. However, SIMD achieves significantly better performance in GFLOPS/sec due to its ability to utilize compute resources more efficiently:

• Parallelism: SIMD leverages AVX-512 vector instructions, which can perform 16 operations per cycle, compared to scalar instructions in the naive implementation.
• Reduced Compute Bottlenecks: By executing multiple operations in a single instruction, SIMD minimizes the time spent on computation, resulting in faster runtimes.
• Compute Efficiency: SIMD achieves higher throughput within the same memory bandwidth constraints, leading to improved performance.

Experimental Results and Plot

The Roofline chart below illustrates the performance of naive and SIMD implementations relative to the memory and compute roofs:

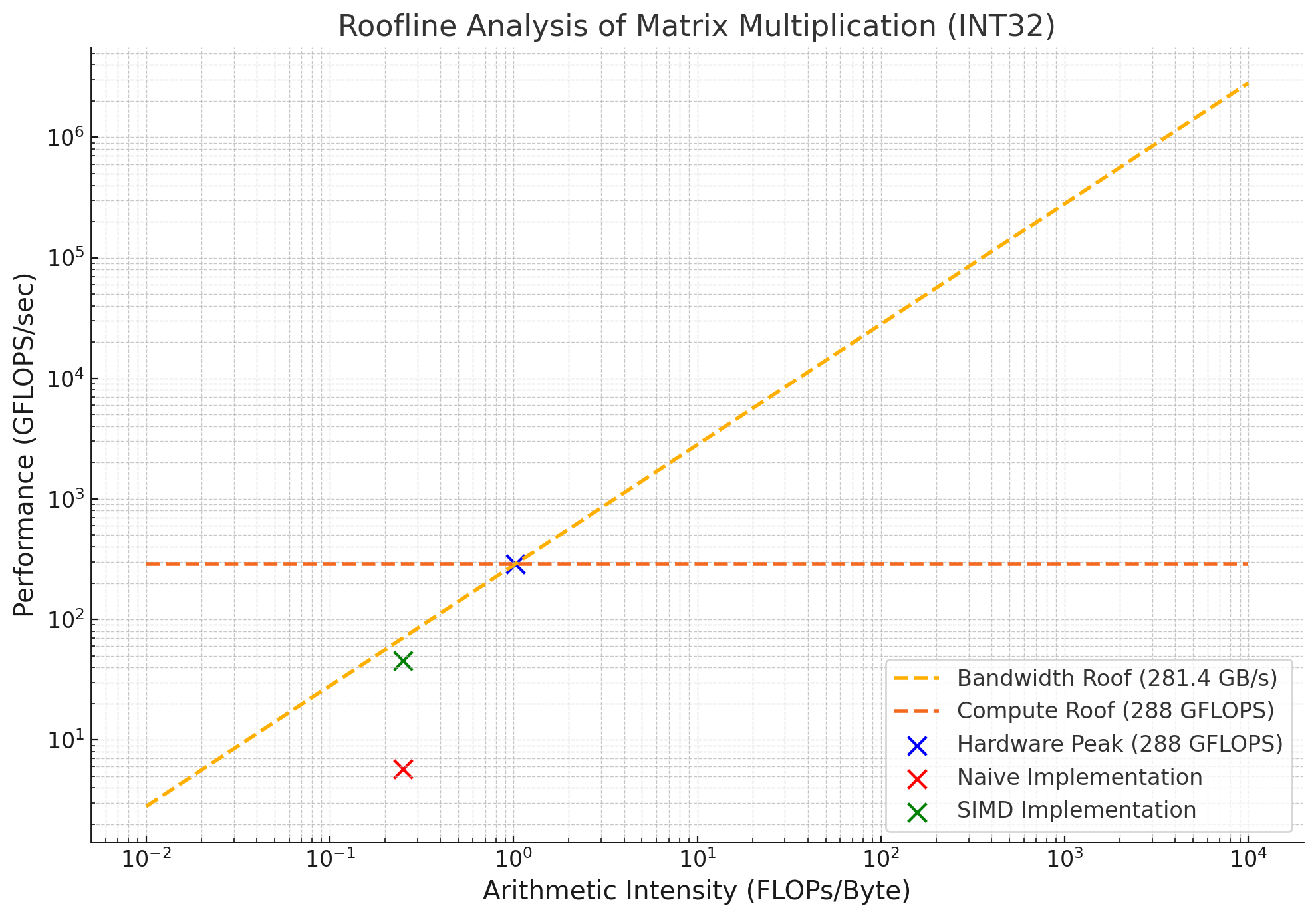
Both implementations are memory-bound due to the low experimental AI (0.249985 FLOPs/byte compared to the hardware AI of 1.02 FLOPs/byte). However, SIMD achieves a significantly better runtime by efficiently utilizing the available compute resources.